[JAVA] 그래프 구현하기 (인접 리스트, 인접 행렬)

그래프

 그래프는 정점(Vertex, Node)과 간선(Edge)으로 이루어진 데이터 구조이다.

 

그래프의 종류

1. 무방향 그래프(Undirected Graph)
   • 간선에 방향이 없는 그래프로, 두 정점 사이의 연결이 쌍방향으로 되어있다.
2. 방향 그래프(Directed Graph)
   • 간선에 방향이 있는 그래프로, 한 정점에서 다른 정점으로의 방향이 정해져 있다.
3. 비가중치 그래프(Unweighted Graph)
   • 간선에 가중치(비용, 거리 등)가 없는 그래프이다.
4. 가중치 그래프(Weighted Graph)
   • 간선에 가중치가 할당된 그래프이다.

이 외에도 순환 그래프(Cyclic Graph), 비순환 그래프(Acyclic Graph) 등이 존재한다.

 

인접 행렬(Adjacency Matrix)

 인접 행렬은 각 정점들이 연결되어 있는 정보를 정사각행렬을 이용해서 나타낸 것이다.

 

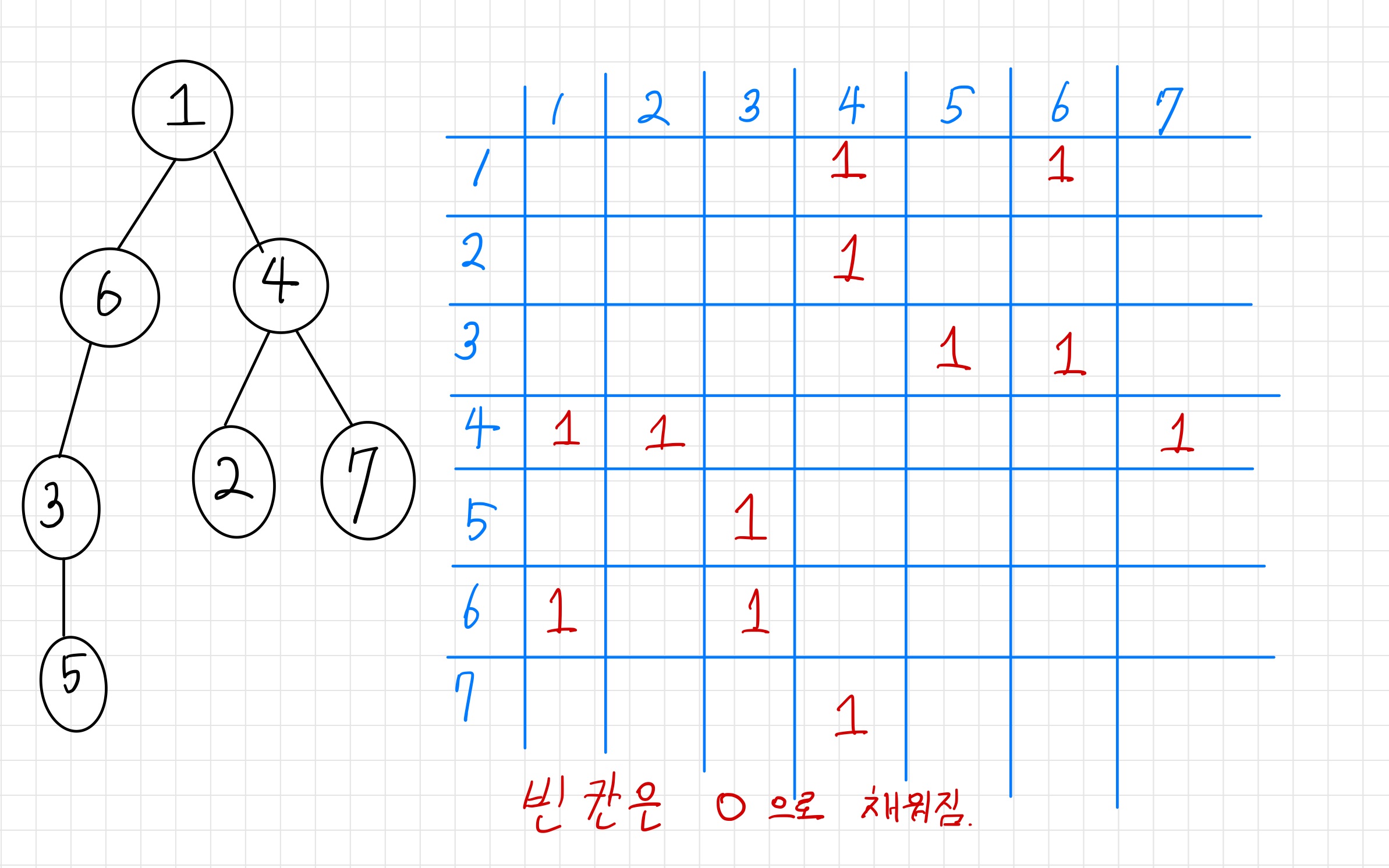
인접 리스트(Adjacency List)

 인접 리스트는 한 정점과 연결되어 있는 정점들을 연결 리스트로 관리하는 방법이다.

 

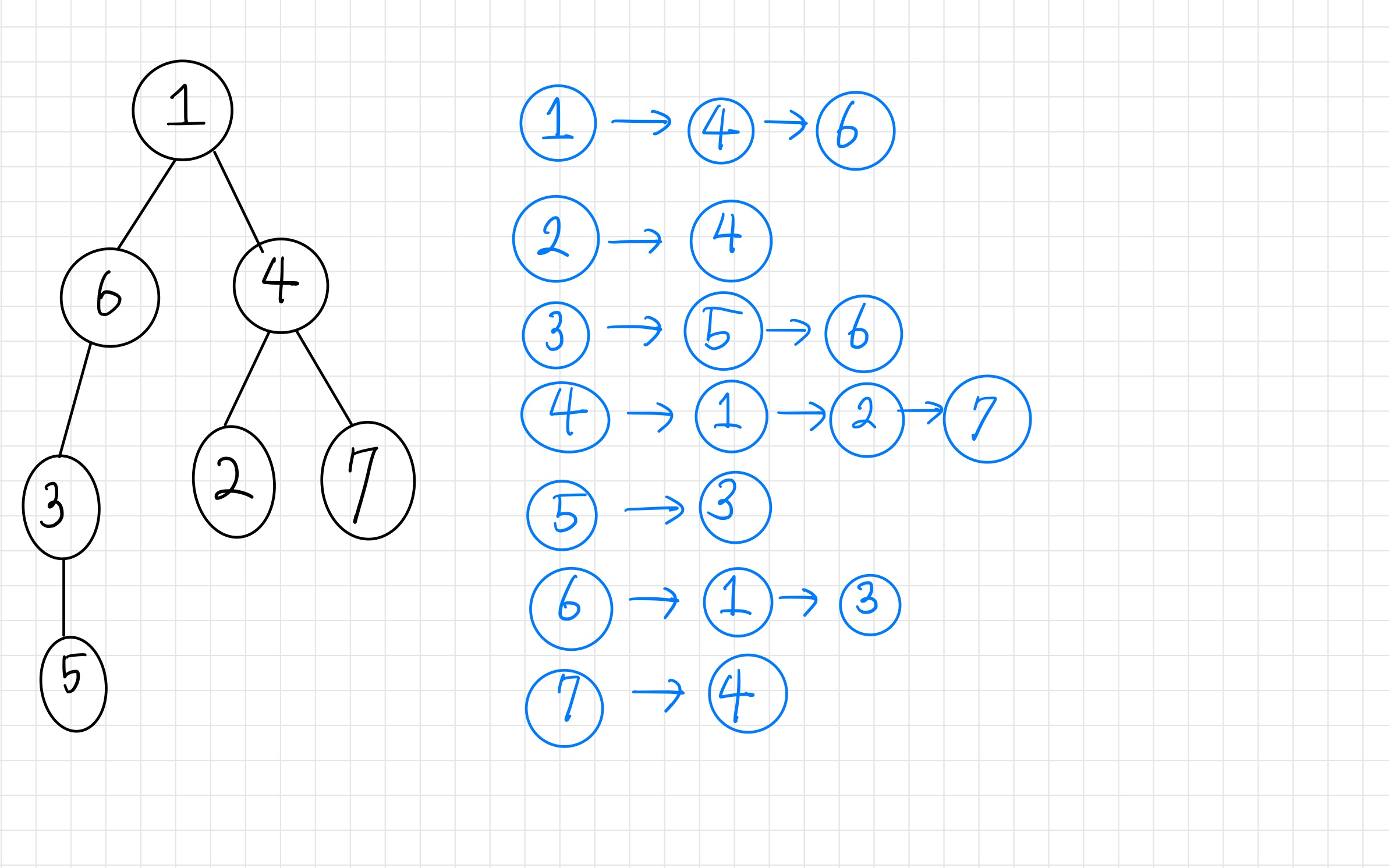
인접 행렬과 인접 리스트 비교

	인접 행렬	인접 리스트
시간 복잡도 (N개의 정점, E개의 간선)	O(N^2)	O(N + E)
효율적인 그래프 구조	밀집 그래프	희소 그래프

 

자바를 이용한 문제 풀이

 백준 1260 : DFS와 BFS

// 인접 행렬
import java.io.*;
import java.util.*;

public class Main {

    static int N, M, V;
    static int[][] board;
    static boolean[] visited;
    static List<Integer> dfsList = new ArrayList<>();
    static List<Integer> bfsList = new ArrayList<>();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        V = Integer.parseInt(st.nextToken());

        board = new int[N + 1][N + 1]; // adjacency matrix

        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());

            board[a][b] = 1;
            board[b][a] = 1;
        }

        visited = new boolean[N + 1];
        dfs(V);
        visited = new boolean[N + 1];
        bfs(V);

        for (int i : dfsList) {
            bw.write(i + " ");
        }
        bw.write("\n");

        for (int i : bfsList) {
            bw.write(i + " ");
        }

        bw.flush();
    }

    public static void dfs(int v) {
        if (visited[v]) {
            return;
        }

        visited[v] = true;
        dfsList.add(v);

        for (int i = 1; i <= N; i++) {
            if (board[v][i] == 1 && !visited[i]) {
                dfs(i);
            }
        }
    }

    public static void bfs(int v) {
        Queue<Integer> queue = new LinkedList<>();

        queue.add(v);
        visited[v] = true;

        while (!queue.isEmpty()) {
            int current = queue.poll();
            bfsList.add(current);

            for (int i = 1; i <= N; i++) {
                if (board[current][i] == 1 && !visited[i]) {
                    queue.add(i);
                    visited[i] = true;
                }
            }
        }
    }

}

// 인접 리스트
import java.io.*;
import java.util.*;

public class Main {

    static int N, M, V;
    static List<List<Integer>> board;
    static boolean[] visited;
    static List<Integer> dfsList = new ArrayList<>();
    static List<Integer> bfsList = new ArrayList<>();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        V = Integer.parseInt(st.nextToken());

        board = new ArrayList<>(); // adjacency list
        for (int i = 0; i <= N; i++) {
            board.add(new ArrayList<>());
        }

        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());

            board.get(a).add(b);
            board.get(b).add(a);
        }

        for (int i = 1; i <= N; i++) {
            Collections.sort(board.get(i));
        }

        visited = new boolean[N + 1];
        dfs(V);
        visited = new boolean[N + 1];
        bfs(V);

        for (int i : dfsList) {
            bw.write(i + " ");
        }
        bw.write("\n");

        for (int i : bfsList) {
            bw.write(i + " ");
        }

        bw.flush();
    }

    public static void dfs(int v) {
        if (visited[v]) {
            return;
        }

        visited[v] = true;
        dfsList.add(v);

        for (int i : board.get(v)) {
            if (!visited[i]) {
                dfs(i);
            }
        }
    }

    public static void bfs(int v) {
        Queue<Integer> queue = new LinkedList<>();

        queue.add(v);
        visited[v] = true;

        while (!queue.isEmpty()) {
            int current = queue.poll();
            bfsList.add(current);

            for (int i : board.get(current)) {
                if (!visited[i]) {
                    queue.add(i);
                    visited[i] = true;
                }
            }
        }
    }

}